A (very short) introduction to Machine Learning

A (very short) introduction to Machine Learning#

Machine Learning (ML) is the set of all techniques and algorithms enabling the extraction of knowledge from data and the use of that knowledge to produce accurate predictions.

Following the above definition, it is clear that a good Machine Learning algorithm requires a few steps:

  • Understanding: Understanding the task (e.g. what do we need? what are the informations we are able to collect, to answer some question?);

  • Collection: Collecting a suitable amount of data, containing enough informations to achieve the task;

  • Design: Designing the Machine Learning algorithm, based on the knowledge of the problem at hand;

  • Training: Training the algorithm on the collected data, trying to minimize the prediction error on a certain part of the data;

  • Tuning: Possibly tuning the parameters of the model (a ML algorithm is usually referred to as model), so to improve the predictions;

  • Testing: Testing the algorithm on another part of the data, verifying the correctness of its predictions;

In the following, we are going to investigate each of these steps more deeply.

Understanding#

Let us assume we want to solve a given problem. Mathematically, the problem can be modelled as an (unknown) function \(f(x)\), taking as input a vector \(x \in \mathbb{R}^d\) - containing the informations we are able to collect - and mapping them (possibly stocastically) to the task \(y = f(x)\). In this context, \(x\) is usually called input vector or alternatively feature vector, while \(y = f(x)\) is the target (equivalently label or output).

Solving Solving the problem means to be able to approximate \(f(x)\) as well as possible through a model (which we will always indicate as \(f_\theta (x)\), \(\theta\) being the set of its parameters), such that

\[ f_\theta(x) \approx f(x) \qquad \forall x \in \mathbb{R}^d \]

Is it learnable?#

A problem \(y = f(x)\) can be solved by a ML algorithm if and only if there exists a relationship between \(x\) and \(y\). For example, we cannot expect to predict the future weather in a particular position by using informations about the stock price of a particular company. In that situation, the input and the output are clearly independent, and there is nothing to learn on one using the other.

As a consequence, while designing a ML algorithm, the first thing to understand is if there exists a correlation between the input and the output, for the given problem. When this is the case, we say that the problem is learnable.

Machine Learning is about understanding correlations (patterns).

It is possible to collect them?#

Let us assume that the problem \(y = f(x)\) is learnable. We need to understand if we can physically collect enough data \(x\), to be able to understand the relationship between it and the corresponding \(y\).

For example, if we want to use ML to make cancer diagnosis on patients, clearly the best way to do that is to use as input the clinical results of any possible medical exam on any patient. Of course, even if this would work well in practice, it is not possible (nor ethical) to test a patient with thousands of exams, for a single diagnosis.

Moreover, in order to train a good ML model, we may need thousands (or sometimes milions) of datapoints, but it is not always possible to scale up the problem, so to be able to collect enough data to solve it.

Collecting data requires efficiency and scalability of the problem.

Collection#

Collecting data is usually the hardest part in the design of a Machine Learning production. In fact, even knowing that our problem \(y = f(x)\) is solvable and that it is theoretically possible to collect enough data about it, it may not always be so easy to do it, in practice.

In particular, some data requires time to be collected (for example, when working in biological or medical applications) and collecting good quality data is hard. Indeed, ideally we want to use a clean dataset, where all the required information is present, there are no missing values (usually referred to as NaN) and there is no noise. Most of the time, achieving this is hopeless and therefore we need to develop algorithms to standardize and clean up the data. The set of all such techniques is called data cleaning, but its study is beyond the scope of this course.

Kaggle#

Luckily, for most of the tasks you can think of, you can find datasets already available on the internet. For example, on websites like Kaggle and Google Datasets .

Data loading with pandas#

At the end of the introductory post we introduced the Python library pandas, useful to work with data.

In particular, most of the data can be found in the .csv format and pandas contains functions to read and work with those files. Please refer to the introductory post for more informations about this.

Datasets and numpy arrays#

.csv datasets are great. While working with them, we always have all the informations correctly labeled and in-place. Unfortunately though, from a mathematical point of view, this is a really sub-optimal way of working with data. In particular, working with strings is usually a pain and it is mandatory to setup an algorithm converting them into numbers (an encoding algorithm); moreover, names of columns and rows are unnecessary while designing learning algorithms.

Consequently, we must always convert datasets into matrices (in the form of numpy arrays), before starting to work with them. This is performed in two successive steps:

  1. encoding strings into numbers;

  2. converting the resulting dataset into a numpy array.

Encoding algorithms are based on the idea that in a dataset, the set of possible values that a string can have is limited (e.g. in a dataset containing weather informations, we can say that the climate is {raining, sunny, cloudy, snowy}, thus we have only 4 possible values for that string). Consequently, the right approach is to consider each one of the possible values as a class.

Let us assume that our dataset has \(K\) classes for a specific feature, denoted as \(\{ C_1, C_2, \dots, C_K \}\). Then, there are two mainly used encoding algorithms:

  • Integer encoding: Each class \(C_k\), \(k = 1, \dots, K\), is simply mapped to its index \(k\) (Warning: this method may create an unintended ordering on the classes, i.e. \(C_k \leq C_j\) if \(i < j\)). In Python, this function is implemented by the function sklearn.preprocessing.LabelEncoder() from sklearn, a famous library performing ML operations.

  • One-hot-encoding: Each class \(C_k\) is mapped to the \(K\)-dimensional canonical vector \(e_k\), where \(e_i\) is a vector of all zeros except for the \(k\)-th element, which is equal to 1 (Advantages: in this way we can define the concept of being partially in a class). In Python, this function is implemented by the function sklearn.preprocessing.OneHotEncoder().

After the encoding step, the dataset is simply converted to a numpy array with the np.array() function.

The result of this procedure is a matrix

\[ X = [ x^1 \quad x^2 \quad \dots \quad x^N ] \in \mathbb{R}^{d \times N} \]

where each column \(x^i \in \mathbb{R}^d\) represents a datapoint with \(d\) features and \(N\) is the number of datapoints. The corresponding labels \(y^i = f(x^i)\) for each datapoint are collected into a vector \(Y = [y^1, y^2, \dots, y^N]^T \in \mathbb{R}^N\)

Design#

Designing a ML model is hard and beyond the scope of this course. For our purposes, it is sufficient to understand the main classification of ML algorithms: supervised and unsupervised learning.

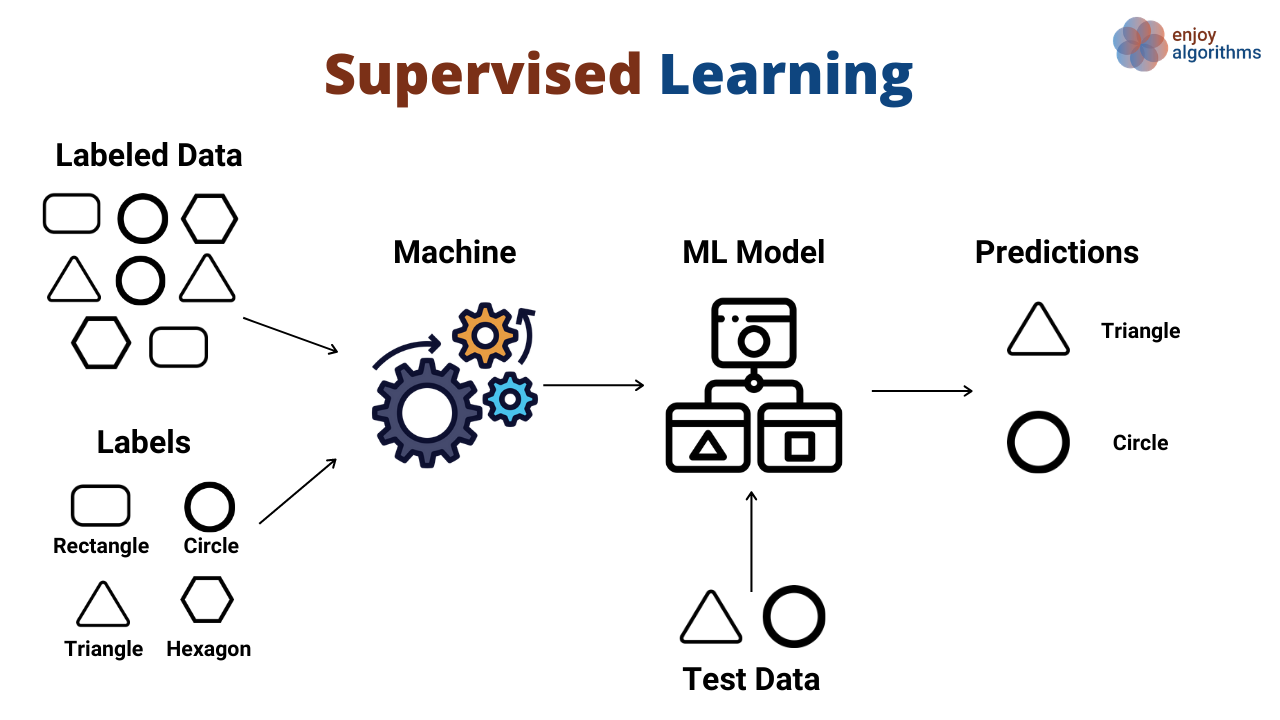
Supervised Learning#

In Supervised Learning (SL), we are given a dataset composed by a set of inputs \(X \in \mathbb{R}^{d \times N}\) and the corresponding labels \(Y \in \mathbb{R}^N\). The core idea of SL techniques is to use informations contained in \(X\) and \(Y\) to learn structures in the data so that, after the training, we can estimate new values of \(y = f(x)\) given a new \(x \in \mathbb{R}^d\).

Unsupervised Learning#

In Unsupervised Learning (UL), we are given a dataset composed by only the inputs \(X \in \mathbb{R}^{d \times N}\), without any corresponding labels. The task of UL techniques is to learn a pattern present in the data with the intent to classify new datum \(x \in \mathbb{R}^d\) by retrieving its patterns.

Training#

Training is the easiest part in the design of ML algorithms. In it, we just use informations contained in the data we have to let our model learn the patterns required to make accurate predictions. We are going to carry out a training experiment soon, which will make clearer how it works.

Tuning#

Every ML algorithms has a limited number of parameters that the user has to set. Generally, those parameters can change the flexibility of the model, making it more or less flexible, depending on the task.

Tuning those parameters is important to improve the accuracy of the algorithm. This is mainly a trial-and-error procedure, whereby the user tries to change the parameters (usually, with knowledge on what they do), trains the model again, checks the performance and changes the parameters again, until the model produces good results.

The concept of flexibility is strongly related to the concept of overfitting and underfitting.

Testing#

Testing the prediction abilities of a ML model on the same dataset on which it has been trained is unfair. Indeed, on those data the model already observed the real outcome and a model performing well on the training set potentially just memorized the informations contained in that set, without understanding any knowledge. For this reason, it is important to keep a portion of the dataset unused in the Training and Tuning phases, but use it to test the model. In particular, when we have \(N\) available data, it is common to select a certain number \(N_{train} < N\) of random samples from \(X\) and use only those data for training and tuning. The remaining \(N_{test} = N - N_{train}\) data can then be used for testing.

Testing is usually realized by choosing an accuracy function \(\ell(y, y')\) and evaluating its mean value over the test set. \(\ell(y, y')\) is computed by comparing the prediction of the trained model \(y = f_\theta(x)\) and the true label \(y' = f(x)\), for the same datum \(x \in \mathbb{R}^d\).

For example, in the clustering example we are going to investigate, \(f(x)\) could be the function associating each point to the corresponding cluster, while \(f_\theta(x)\) maps the input data \(x\) to an estimate of its potential cluster. When this is the case, we can define the accuracy of the model as the number of datapoints mapped to the correct cluster. In particular, if \(k_x = f(x)\), \(k = 1, \dots, K\) is the cluster associated with \(x \in \mathbb{R}^n\), then for any \(x\),

\[\begin{split} \ell(f_\theta(x), k_x) = \begin{cases} 1 \qquad \text{if } f_\theta(x) \neq k_x \\ 0 \qquad \text{if } f_\theta(x) = k_x\end{cases} \end{split}\]

If \(\mathcal{S} = \{ (x_i, k_{x_i}) \}\), \(i= 1, \dots, N_{test}\) is the test set (as defined in the section above), then the accuracy of the model \(f_\theta(x)\) is

\[ Acc(f_\theta) = \frac{1}{N_{test}} \sum_{i=1}^{N_{test}} \ell (f_\theta(x_i), k_{x_i}) \]

usually referred as misclassification rate. In the following, we are going to implement this in Python.

Contents